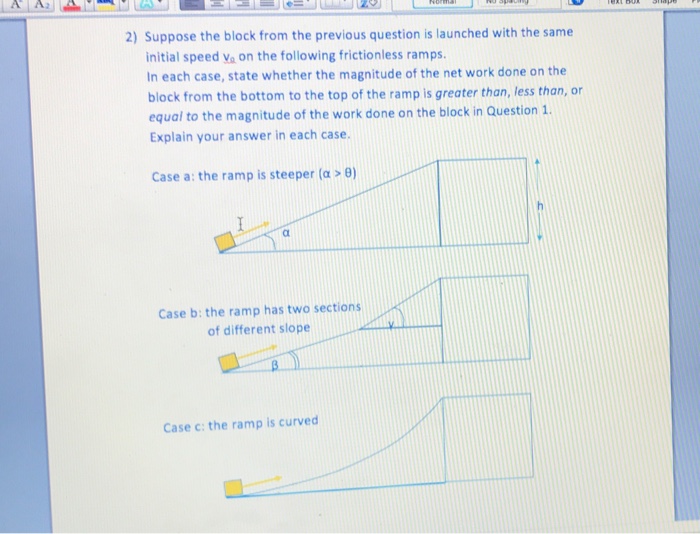
A block is projected up a frictionless plane, embarking on a captivating journey that reveals the intricate interplay of forces and motion. This exploration delves into the kinematics, force analysis, and graphical representation of the block’s trajectory, unraveling the fundamental principles governing its ascent and descent.
The angle of inclination sets the stage for the block’s motion, influencing its velocity, acceleration, and displacement. The absence of friction eliminates resistance, allowing the block to move freely under the influence of gravity and the normal force exerted by the plane.
A Block Projected Up a Frictionless Plane: A Block Is Projected Up A Frictionless Plane
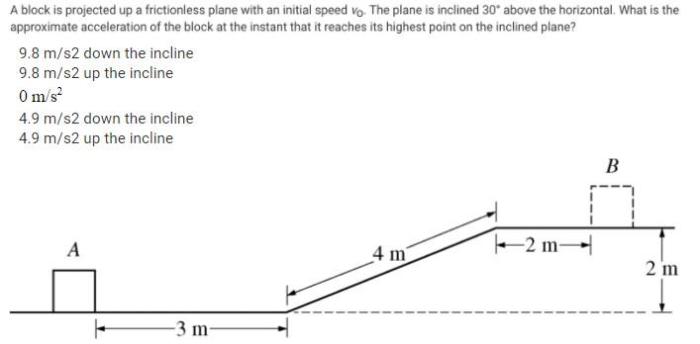
In physics, the motion of a block projected up a frictionless plane is a fundamental concept that demonstrates the principles of kinematics, dynamics, and energy conservation.
Problem Definition
Consider a block of mass m initially projected up a frictionless plane inclined at an angle θ to the horizontal. The block’s initial velocity is v iat a height h above the base of the plane.
Kinematic Analysis, A block is projected up a frictionless plane
The block’s motion can be described by the following equations of motion:
- Velocity components: v x= v icosθ, v y= -v isinθ
- Acceleration components: a x= 0, a y= -g
- Displacement: x = v icosθt, y = -v isinθt + 1/2gt 2
The angle of inclination affects the block’s motion by reducing the acceleration due to gravity along the inclined plane, which in turn affects the block’s velocity and displacement.
The conservation of energy principle states that the total energy of the block remains constant throughout its motion. The initial potential energy of the block is converted into kinetic energy as it moves up the plane and then back into potential energy as it descends.
Force Analysis
The forces acting on the block are:
- Gravity: mg, directed vertically downward
- Normal force from the plane: N, directed perpendicular to the plane
The normal force balances the component of gravity perpendicular to the plane, while the component of gravity parallel to the plane causes the block to accelerate up or down the plane.
The relationship between the forces and the block’s acceleration is given by Newton’s second law: ma = F net.
Graphical Representation
A velocity-time graph can be used to illustrate the block’s motion. The graph shows that the block’s velocity decreases as it moves up the plane and increases as it descends.
A table can be used to organize the relevant data, such as velocity, acceleration, and displacement, at different points in time.
Applications
The concept of a block projected up a frictionless plane has numerous applications in real-world scenarios, including:
- Projectile motion: A projectile launched into the air can be analyzed using the same principles as a block projected up a frictionless plane.
- Inclined planes: The motion of objects on inclined planes is often analyzed using the same principles, taking into account the angle of inclination.
- Engineering: The principles governing the motion of objects on inclined planes are used in the design of ramps, conveyor belts, and other mechanical systems.
Question & Answer Hub
What is the significance of the angle of inclination in this scenario?
The angle of inclination plays a crucial role in determining the block’s acceleration and trajectory. A steeper angle results in a greater component of gravity acting along the plane, leading to a higher acceleration and a shorter flight time for the block.
How does the conservation of energy principle apply to the block’s motion?
The conservation of energy principle states that the total energy of the block remains constant throughout its motion. As the block ascends the plane, its kinetic energy is converted into potential energy due to its increasing height. Conversely, as it descends, its potential energy is transformed back into kinetic energy.
What practical applications can be derived from understanding this concept?
Understanding the dynamics of a block projected up a frictionless plane has practical applications in various fields. It helps engineers design ramps and slopes for efficient movement of objects, and physicists analyze projectile motion and inclined plane experiments. It also provides insights into the behavior of objects moving on inclined surfaces in everyday situations, such as cars driving up hills or objects sliding down slides.