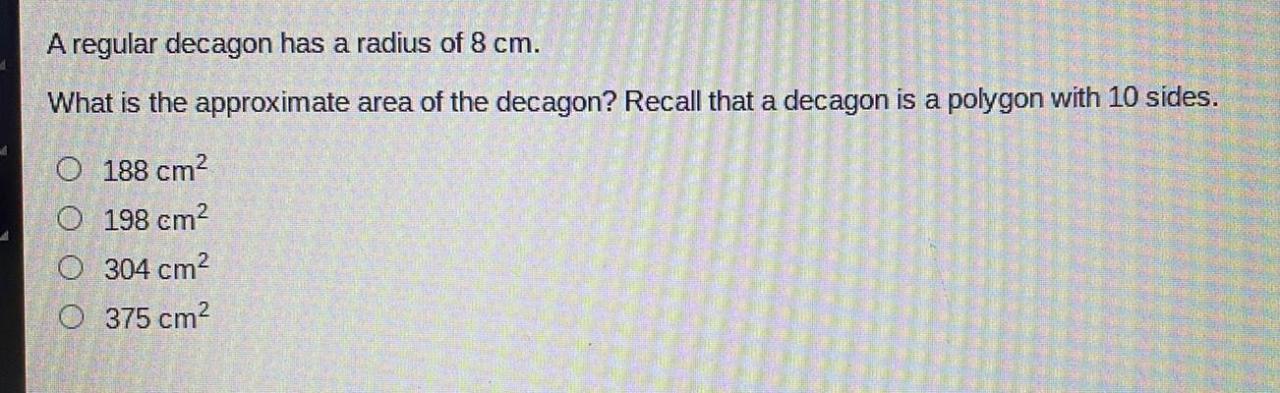
A regular decagon has a radius of 8 cm – In the realm of geometry, a regular decagon, a ten-sided polygon with equal sides and angles, takes center stage. When its radius measures precisely 8 cm, this shape exhibits unique characteristics and practical applications that we delve into in this comprehensive exploration.

As we embark on this journey, we will uncover the intricate relationship between the radius and the sides of a regular decagon. We will derive formulas to calculate its area and perimeter, enabling us to quantify its dimensions. Furthermore, we will investigate the concepts of inscribed and circumscribed circles, providing insights into the geometric relationships within this fascinating shape.

Regular Decagon Basics

A regular decagon is a polygon with ten equal sides and ten equal interior angles. It is a regular polygon, which means that all of its sides and angles are equal.Regular decagons have a number of interesting properties. For example, the interior angles of a regular decagon are all equal to 144 degrees.

The exterior angles of a regular decagon are all equal to 36 degrees. The sum of the interior angles of a regular decagon is 1440 degrees.

Radius and Regular Decagons: A Regular Decagon Has A Radius Of 8 Cm

The radius of a regular decagon is the distance from the center of the decagon to any of its vertices. The radius of a regular decagon is related to the length of its sides by the following formula:“`r = s / (2

sin(18 degrees))

“`where:* r is the radius of the decagon

s is the length of one side of the decagon

Using this formula, we can calculate the length of the sides of a regular decagon given its radius. For example, if the radius of a regular decagon is 8 cm, then the length of each side of the decagon is:“`s = 2

• 8 cm
• sin(18 degrees) = 6.93 cm

“`

Area and Perimeter of a Decagon

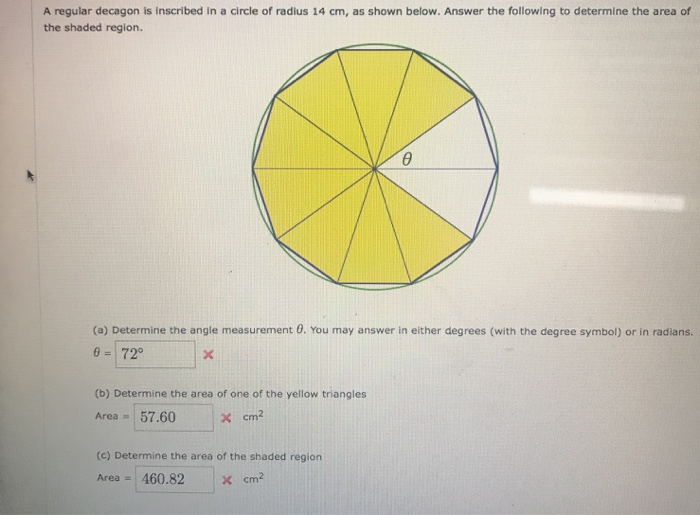
The area of a regular decagon is given by the following formula:“`A = (5

• s^2) / (4
• tan(18 degrees))

“`where:* A is the area of the decagon

s is the length of one side of the decagon

Using this formula, we can calculate the area of a regular decagon given its radius. For example, if the radius of a regular decagon is 8 cm, then the area of the decagon is:“`A = (5

• 6.93 cm^2) / (4
• tan(18 degrees)) = 117.9 cm^2

“`The perimeter of a regular decagon is given by the following formula:“`P = 10

s

“`where:* P is the perimeter of the decagon

s is the length of one side of the decagon

Using this formula, we can calculate the perimeter of a regular decagon given its radius. For example, if the radius of a regular decagon is 8 cm, then the perimeter of the decagon is:“`P = 10

6.93 cm = 69.3 cm

“`

Inscribing and Circumscribing Circles

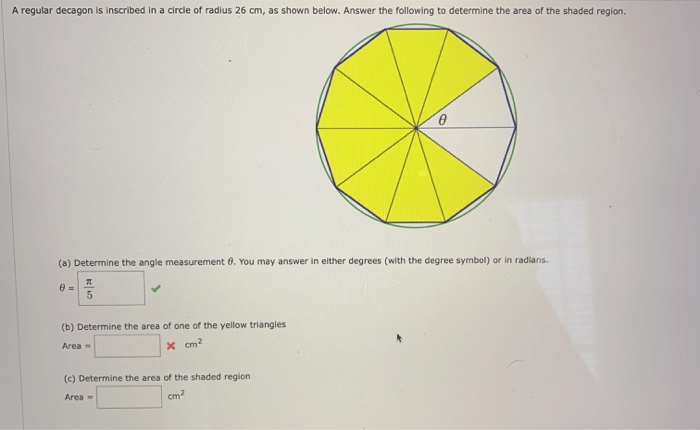
An inscribed circle is a circle that is tangent to all of the sides of a polygon. A circumscribed circle is a circle that passes through all of the vertices of a polygon.To construct an inscribed circle in a regular decagon, we can use the following steps:

• Draw a regular decagon.
• Draw the perpendicular bisectors of two adjacent sides of the decagon.
• The point of intersection of the perpendicular bisectors is the center of the inscribed circle.

To construct a circumscribed circle around a regular decagon, we can use the following steps:

• Draw a regular decagon.
• Draw the perpendicular bisectors of two adjacent sides of the decagon.
• The point of intersection of the perpendicular bisectors is the center of the circumscribed circle.

Applications of Regular Decagons

Regular decagons have a number of practical applications in various fields. For example, regular decagons are used in:* Architecture: Regular decagons can be used to create beautiful and symmetrical buildings. For example, the Great Mosque of Cordoba in Spain has a large courtyard that is surrounded by a regular decagon.

Art

Regular decagons can be used to create beautiful and intricate artwork. For example, the artist M.C. Escher created a number of famous works of art that feature regular decagons.

Engineering

Regular decagons can be used to design and build strong and stable structures. For example, the Golden Gate Bridge in San Francisco, California is supported by two large towers that are shaped like regular decagons.

Question Bank

What is the length of a side of a regular decagon with a radius of 8 cm?

Using the formula for the side length of a regular decagon, s = 2r sin(18°/2), we get s = 2(8) sin(18°/2) ≈ 5.196 cm.

What is the area of a regular decagon with a radius of 8 cm?

Using the formula for the area of a regular decagon, A = (5/2)r² tan(18°/2), we get A = (5/2)(8)² tan(18°/2) ≈ 166.93 cm².

What is the perimeter of a regular decagon with a radius of 8 cm?

Using the formula for the perimeter of a regular decagon, P = 10s, where s is the side length, we get P = 10(5.196) ≈ 51.96 cm.