Parallel lines e and f are cut by transversal b, revealing a fascinating interplay of angles and properties that form the cornerstone of geometry. This intersection unveils a wealth of relationships and applications, making it an essential concept in various fields.
As we delve into the intricacies of parallel lines and transversals, we will explore the types of angles formed, their properties, and their practical significance. By understanding these concepts, we gain a deeper appreciation for the elegance and power of geometry.
Parallel Lines and Transversals
Parallel lines are lines that never intersect, no matter how far they are extended. A transversal is a line that intersects two or more parallel lines.
Angles Formed by Parallel Lines and Transversals, Parallel lines e and f are cut by transversal b
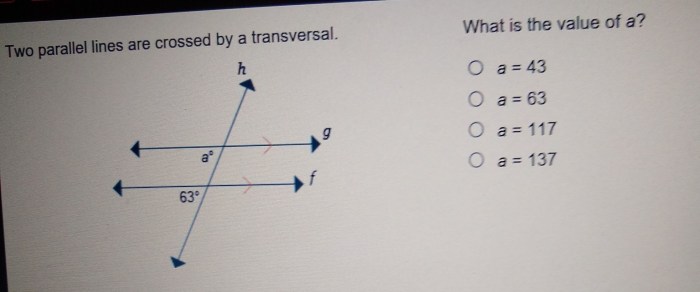
When parallel lines are cut by a transversal, eight angles are formed. These angles are classified into four types:
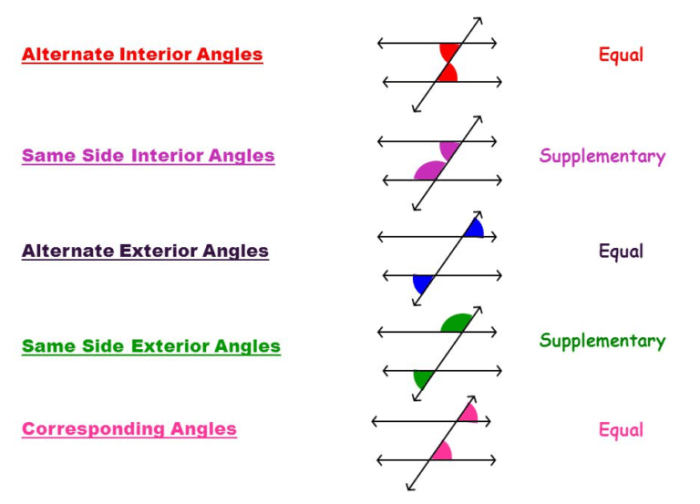
- Alternate interior angles: These are the angles that are on opposite sides of the transversal and inside the parallel lines.
- Alternate exterior angles: These are the angles that are on opposite sides of the transversal and outside the parallel lines.
- Corresponding angles: These are the angles that are on the same side of the transversal and in the same position relative to the parallel lines.
- Same-side interior angles: These are the angles that are on the same side of the transversal and inside the parallel lines.
The relationships between these angles are as follows:
| Angle Type | Relationship |
|---|---|
| Alternate interior angles | Congruent |
| Alternate exterior angles | Congruent |
| Corresponding angles | Congruent |
| Same-side interior angles | Supplementary |
Properties of Parallel Lines and Transversals
- If two lines are parallel to a third line, then they are parallel to each other.
- If a transversal intersects two parallel lines, then the alternate interior angles are congruent.
- If a transversal intersects two parallel lines, then the alternate exterior angles are congruent.
- If a transversal intersects two parallel lines, then the corresponding angles are congruent.
- If a transversal intersects two parallel lines, then the same-side interior angles are supplementary.
Applications of Parallel Lines and Transversals
Parallel lines and transversals are used in a variety of applications, including:
- Architecture: Parallel lines are used to create the walls and roofs of buildings. Transversals are used to create windows and doors.
- Engineering: Parallel lines are used to create bridges and other structures. Transversals are used to create supports and braces.
- Surveying: Parallel lines and transversals are used to measure distances and angles.
- Navigation: Parallel lines and transversals are used to create maps and charts.
Common Queries: Parallel Lines E And F Are Cut By Transversal B
What are parallel lines?
Parallel lines are lines that never intersect, no matter how far they are extended.
What is a transversal?
A transversal is a line that intersects two or more other lines.
What types of angles are formed when parallel lines are cut by a transversal?
When parallel lines are cut by a transversal, four types of angles are formed: corresponding angles, alternate interior angles, alternate exterior angles, and same-side interior angles.