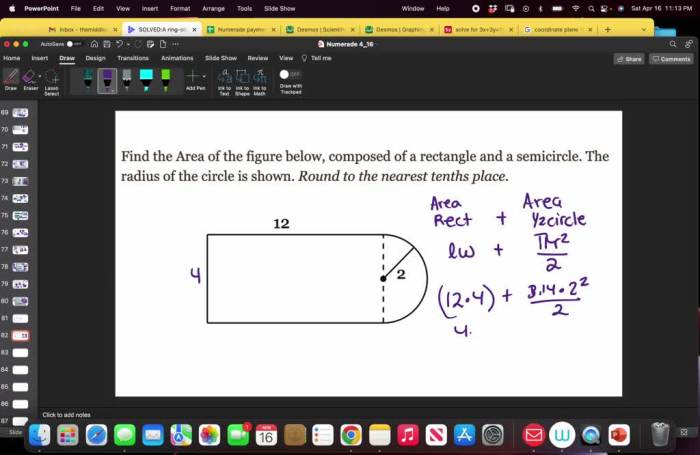
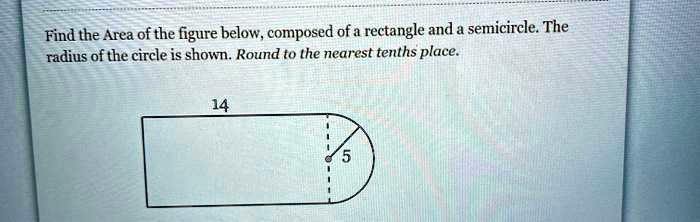
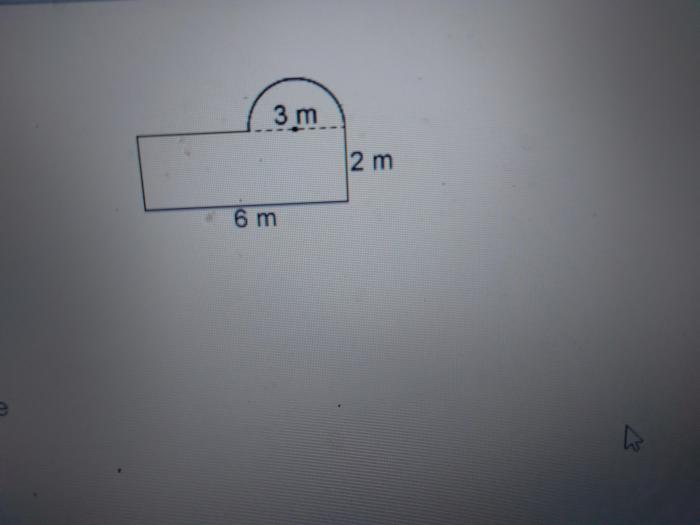
The figure shown is a rectangle with a semicircle, a captivating geometric combination that unveils a rich tapestry of mathematical concepts. This figure, composed of two distinct shapes, presents a unique opportunity to delve into the realms of geometry, exploring its properties, applications, and the intriguing relationship between its constituent parts.
The rectangle, with its straight sides and right angles, provides a foundation of stability and order. The semicircle, on the other hand, introduces an element of fluidity and grace, its curved edge inviting exploration and contemplation. Together, these shapes create a harmonious union that showcases the beauty and versatility of geometric forms.
Rectangle and Semicircle: Geometric Analysis
In geometry, a rectangle and a semicircle can be combined to form a composite figure. This combination has unique geometric properties and practical applications in various fields.
Rectangle Description
A rectangle is a two-dimensional shape with four straight sides and four right angles. The opposite sides of a rectangle are parallel and equal in length.
Area and Perimeter
The area (A) of a rectangle is calculated as follows:
A = length (l) × width (w)
The perimeter (P) of a rectangle is the sum of the lengths of all four sides:
P = 2l + 2w
Relationship between Length and Width
The length (l) and width (w) of a rectangle are related such that:
l ≠ w
This means that the length and width of a rectangle are always different, making it a non-square rectangle.
Semicircle Description
A semicircle is a half-circle, formed by cutting a circle in half along a diameter. It consists of a curved arc and two straight radii.
Area and Circumference
The area (A) of a semicircle is calculated as follows:
A = (πr²) / 2
where r is the radius of the semicircle.
The circumference (C) of a semicircle is the sum of the length of the arc and the diameter:
C = πr + 2r
Relationship between Radius and Diameter
The radius (r) and diameter (d) of a semicircle are related such that:
d = 2r
This means that the diameter of a semicircle is always twice the length of its radius.
Combined Figure Analysis, The figure shown is a rectangle with a semicircle
In the given figure, the rectangle and semicircle are combined such that the diameter of the semicircle is equal to the length of the rectangle.
Total Area
The total area (A) of the combined figure is the sum of the area of the rectangle and the area of the semicircle:
A = l × w + (πr²) / 2
Total Perimeter
The total perimeter (P) of the combined figure is the sum of the perimeter of the rectangle and the circumference of the semicircle:
P = 2l + 2w + πr + 2r
Geometric Properties
The combined figure has a number of geometric properties, including:
- Symmetry: The figure is symmetrical about the vertical axis passing through the center of the semicircle.
- Curvature: The semicircle introduces curvature into the figure, which is not present in the rectangle.
- Variety of Shapes: By varying the dimensions of the rectangle and the radius of the semicircle, a wide range of shapes can be created.
Applications and Examples
The combined figure of a rectangle and a semicircle has practical applications in various fields, including:
Architecture
- Arched windows and doorways
- Rounded corners in buildings
- Curved roofs and canopies
Engineering
- Bridges with semicircular arches
- Tunnels with rectangular cross-sections and semicircular roofs
- Aircraft wings with rounded tips
Design
- Furniture with curved edges
- Logos and symbols incorporating both rectangular and curved elements
- Textile patterns with alternating rectangular and semicircular motifs
Essential Questionnaire: The Figure Shown Is A Rectangle With A Semicircle
What is the area of a semicircle?
The area of a semicircle is given by the formula: A = (πr²) / 2, where r is the radius of the semicircle.
How do you calculate the perimeter of a rectangle with a semicircle?
The perimeter of a rectangle with a semicircle is equal to the sum of the length of the rectangle, the width of the rectangle, and the circumference of the semicircle: P = 2L + 2W + πr, where L is the length of the rectangle, W is the width of the rectangle, and r is the radius of the semicircle.
What are some real-world applications of the figure of a rectangle with a semicircle?
The figure of a rectangle with a semicircle is used in a variety of real-world applications, including architecture, design, and engineering. For example, it can be found in the design of bridges, arches, and windows.