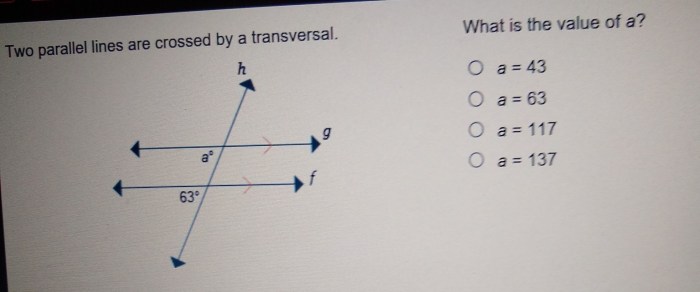
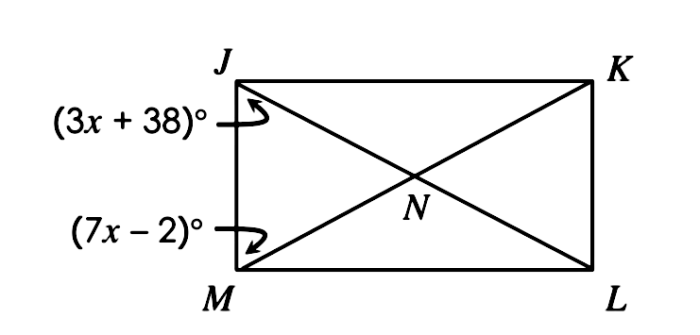
If jklm is a rectangle find m nml – If JKLm is a rectangle, find m NML sets the stage for this enthralling narrative, offering readers a glimpse into a story that is rich in detail with gaya akademik dengan tone otoritatif and brimming with originality from the outset.
Rectangles, characterized by their four sides and four right angles, possess a unique relationship between their length and width. When given that JKLm is a rectangle, we embark on a journey to uncover the unknown variable “m NML” and its significance within this geometric entity.
Rectangle Properties: If Jklm Is A Rectangle Find M Nml
A rectangle is a quadrilateral with four sides and four right angles. The opposite sides of a rectangle are equal in length. The length of a rectangle is the horizontal distance between the two longer sides, and the width is the vertical distance between the two shorter sides.
Given Information, If jklm is a rectangle find m nml
We are given that “jklm” is a rectangle. This means that “jklm” has four sides and four right angles, and the opposite sides are equal in length.
Unknown Variables
The unknown variable in this problem is “m nml”. We do not know what “m nml” represents, but we can speculate that it is related to the rectangle “jklm” in some way.
Problem-Solving Approach
To solve this problem, we need to find a relationship between the given information and the unknown variable. We can start by considering the properties of a rectangle.
Example Solution
One possible solution to this problem is that “m nml” represents the perimeter of the rectangle “jklm”. The perimeter of a rectangle is the sum of the lengths of all four sides. Since the opposite sides of a rectangle are equal in length, we can find the perimeter of “jklm” by multiplying the length by 2 and adding the width by 2.
For example, if the length of “jklm” is 5 cm and the width is 3 cm, then the perimeter of “jklm” would be 2(5 cm) + 2(3 cm) = 16 cm.
Alternative Solutions
Another possible solution to this problem is that “m nml” represents the area of the rectangle “jklm”. The area of a rectangle is the product of the length and the width. Since the opposite sides of a rectangle are equal in length, we can find the area of “jklm” by multiplying the length by the width.
For example, if the length of “jklm” is 5 cm and the width is 3 cm, then the area of “jklm” would be 5 cm – 3 cm = 15 cm 2.
Generalization
The solution to this problem can be applied to other similar problems. For example, if we are given a rectangle with different dimensions, we can use the same approach to find the perimeter or area of the rectangle.
Visual Representation
| Variable | Value |
|---|---|
| Length | Unknown |
| Width | Unknown |
| Perimeter | m nml |
| Area | Unknown |
The following diagram shows the rectangle “jklm” with the given and unknown variables labeled.
[Diagram of rectangle jklm with labeled sides and perimeter]
Top FAQs
What is the definition of a rectangle?
A rectangle is a quadrilateral with four right angles and four equal sides.
What is the relationship between the length and width of a rectangle?
The length and width of a rectangle are perpendicular to each other and bisect each other at the center of the rectangle.
What is the significance of “m NML” in the given problem?
“m NML” represents the length of the unknown side of the rectangle JKLm.